Geometria Espacial
1) A altura de um cone circular reto mede o triplo da medida do raio da base. Se o comprimento da circunferência dessa base é 8πcm, então o volume do cone, em centímetros cúbicos, é
A) 64π
B)60 π
C)55 π
2) Deseja-se construir um cone circular reto com 4cm de raio da base e 3cm de altura. Para isso, recorta-se em cartolina, um setor circular para a superfície lateral e um círculo para a base. A medida do ângulo central do setor circular é:
A) 290º
B) 278º
C) 288°
3) Ao se girar um triangulo retângulo de lados 3m, 4m e 5m em torno da hipotenusa, obtém-se um sólido cujo volume, em m³, é igual a:
A) 60 48π/5
B) 48 48π/5
C) 50 48π/5
4) Um copinho de sorvete em forma de cone tem diâmetro igual a 5cm e altura igual a 15cm. A empresa fabricante diminuiu o diâmetro para 4cm, mantendo a mesma altura. Em quantos por cento variou o volume?
A) diminui 37%
B) diminui 40%
C) diminui 36%
5) Um tronco de pirâmide de bases quadradas tem 21dm³ de volume. A altura do tronco mede 30cm e o lado do quadrado da base maior, 40cm. Então, o lado do quadrado da base menor mede:
A) 10
B) 11
C) 15
6) A base de uma pirâmide tem área igual a 225cm². A 2/3 do vértice, corta-se a pirâmide por um plano paralelo à base. A área da secção é igual a:
A) 200
B) 100
C) 150
7) Um copo de chope é um cone(oco), cuja altura é o dobro do diâmetro da base. Se uma pessoa bebe desde que o copo está cheio até o nível da bebida ficar exatamente na metade da altura do copo, a fração do volume total que deixou de ser consumida é:
A) 1/8
B) 2/8
C) 1/8
8) Um copo de papel, em forma de cone, é formado enrolando-se um semicírculo que tem um raio de 12cm. O volume do copo é de, aproximadamente:
A) 360
B) 386
C) 385cm³
9) Considere um triangulo isósceles ABC, tal que AB = BC = 10cm e CA = 12cm. A rotação desse triangulo em torno de um eixo que contém o lado AC gera um sólido cujo volume, em centímetros cúbicos, é:
A) 250π
B) 258π
C) 256π
10) O volume de uma esfera cresce 72,8% quando o raio dessa esfera aumenta:
A) 19%
B) 20%
C) 30%
11) A intersecção de um plano com uma esfera é um círculo de 16πdm² de área. Sabendo-se que o plano dista 3dm do centro da esfera, o volume da esfera é:
A) 650π/3
B) 600π/3
C) 500π/3
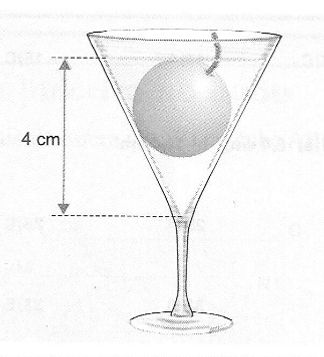
12) Um cálice com a forma de um cone mantém V cm³ de uma bebida. Uma cereja de forma esférica, com diâmetro 2cm, é colocada dentro do cálice, supondo que a cereja repousa apoiada nas laterais do cálice, e o liquido recobre exatamente a cereja a uma altura de 4cm a partir do vértice do cone, determinar o valor de V.
A) 5π/3
B) 4π/3
C) 6π/3
13) Um fuso esférico, cujo ângulo equatorial mede π/3 rad faz parte de uma superfície esférica de 12cm de raio. A área desse fuso esférico, em cm², é igual a:
A) 94π
B) 95π
C) 96π
14) O volume de uma esfera inscrita num cubo cuja aresta mede 6cm é:
A) 36π
B) 39π
C) 40π
15) Um cubo está inscrito uma esfera de raio R. Sua área total é:
A) 8R²
B) 9R²
C) 10R²
16) Em um cilindro reto, de 4m de altura e 0,5m de raio, foi inscrito um prisma quadrangular regular. Qual a razão entre os volumes?
A) π/1
B) π/2
C) π/3
17) Um cilindro está inscrito em um cubo cuja diagonal mede 20cm. Calcule a área lateral do cilindro.
A) 400π/3
B) 500π/3
C) 700π/3
18) No retângulo ABCD, temos AB = 5cm e BC = 2cm. Calcular a área total do sólido gerado pela revolução de 360° da região do retângulo ABCD em torno do eixo e paralelo ao lado AB e distante 1cm de AB como mostra a figura.
A) 53πcm²
B) 55πcm²
C) 56πcm²
19) Qual o valor da área e o volume gerados pela rotação da figura dada em torno do eixo XY?
A) A = 9πa² e V = 3√3 .π.a³/4
B) A = 9πa² e V = 3√3 .π.a³/5
C) A = 9πa² e V = 3√3 .π.a³/6
20) Um prisma triangular tem todas as arestas congruentes e 48m² de área lateral. Seu volume vale:
A) 16√3
B) 17√3
C) 19√3
21) Petróleo matou 270 mil aves no Alasca em 1989
Da redação
O primeiro – e mais grave – acidente ecológico ocorrido no Alasca foi provocado pelo vazamento de 42 milhões de litros de petróleo do navio tanque Exxon Valdez, no dia 24 de março de 1989. O petroleiro começou a vazar após chocar-se com recifes na baia Príncipe Willian. Uma semana depois, 1300km² da superfície do mar já estavam cobertos de petróleo.
Supondo que o petróleo derramada se espalhasse uniformemente nos 1300km² da superfície do mar, a espessura da camada de óleo teria aproximadamente:
A) 0,029mm
B) 0,031mm
C) 0,032mm
22) Qual é a distância entre os centros de duas faces adjacentes de um cubo de aresta 4?
A) 2√2
B) 3√2
C) 4√2
23) Diminuindo-se de 1 unidade de comprimento a aresta de um cubo, o seu volume diminui 61 unidades de volume. A área total desse cubo, em unidades de área é igual a:
A) 140
B) 150
C) 155
24) Se um cubo tem suas arestas aumentadas em 20% cada uma, então seu volume fica aumentado em:
A) 70,8%
B) 71,8%
C) 72,8%
26) Uma caixa d´água tem forma cúbica com 1metro de aresta. De quanto baixa o nível da água ao retirarmos 1 litro de água da caixa?
A) 1mm
B) 2mm
C) 3mm
25) Um paralelepípedo retângulo tem 142 cm² de área total e a soma dos comprimentos de suas arestas vale 60 cm. Sabendo que os seus lados estão em progressão aritmética, eles valem:
A) 1,5,7
B) 2,5,7
C) 3,5,7
26) Um tanque em forma de paralelepípedo tem por base um retângulo horizontal de lados 0,8 m e 1,2 m. Um indivíduo, ao mergulhar completamente no tanque, faz o nível da água subir 0,075m. Então o volume do indivíduo, em litros, é:
A) 72
B) 74
C) 80
27) Se o apótema de uma pirâmide mede 17m e o apótema da base mede 8m, qual é a altura da pirâmide?
A) 15m
B) 18m
C) 20m
28) Qual é a área total de uma pirâmide quadrangular regular, sabendo-se que sua altura mede 24cm e que o apótema da pirâmide mede 26cm?
A) 1430cm²
B) 1440cm²
C) 1445cm²
29) Uma pirâmide quadrada tem todas as arestas medindo 2. A altura mede:
A) √2
B) √6
C) √9
30) As arestas laterais de uma pirâmide reta medem 15cm, e a sua base é um quadrado cujos lados medem 18cm. A altura dessa pirâmide, em cm, é igual a:
A) 2√7
B) 3√7
C) 4√7
31) As projeções ortogonais de um cilindro sobre dois planos perpendiculares são, respectivamente, um círculo e um quadrado. Se o lado do quadrado é 10, qual o volume do cilindro?
A) 248π
B) 249π
C) 250π